Artificial Intelligence (AI) can now solve a mathematical problem, making science simpler. According to the researchers, these partial differential equations PDEs will aid in our understanding of how nature works. Due to their difficulty, the majority of differential equations are difficult to solve.
Partial differential equations can be used in modelling everything from planetary motion to plate tectonics, but they’re extremely difficult to solve. Once solved, however, we can get to the more exciting stuff. You really don’t need to know anything about them unless you’re a physicist or an engineer.
A partial differential equation in mathematics is a type of differential equation in which the equation involves unknown multi variables with partial derivatives. They are a category of math equation that does quite well at explaining changes in space and time, making them useful for describing the physical phenomena that occur in our universe. They can be used to represent anything from planetary orbits to plate tectonics to air turbulence that disrupts flights, allowing us to do things like forecast seismic activity and build safe planes.
The problem is that PDEs are notoriously difficult to solve. And maybe the best way to explain the sense of “solve” is with an example. Assume you’re trying to test a new plane concept by simulating air turbulence. Navier-Stokes is a well-known PDE that is used to describe the motion of any fluid. When you are solving Navier-Stokes, you can take a snapshot of the air’s motion (also known as wind conditions) at any point in time and model how it would continue moving, or how it was moving previously.
The extreme complexity of partial differential equation calculation forces many disciplines that uses partial differential equation a lot to rely on supercomputers to perform their calculation. This is also why these equations have sparked an interest in the AI communities. Using deep learning will help scientific inquiry and engineering a lot if it could speed up the process of solving them.
These calculations are extremely complex and computationally intensive, which is why disciplines that use a lot of partial differential equations often rely on supercomputers to perform the calculations. But, even with supercomputers, the time taken to solve the equations will be extremely long. It’s also why these equations have piqued the interest of the AI community. If deep learning could be used to speed up the process of solving them, it could be extremely beneficial to scientific research and engineering.
Caltech researchers have created a new deep-learning technique for solving PDEs known as the “Fourier Neural Operator for Parametric Partial Differential Equations,” which is significantly more accurate than previous deep-learning approaches. It’s much more generalizable, allowing it to solve an entire family of PDEs without requiring retraining, such as the Navier-Stokes equation for any kind of fluid. Finally, it is 1,000 times faster than conventional mathematical formulas, reducing reliance on supercomputers and allowing us to model even larger problems with greater computational power.
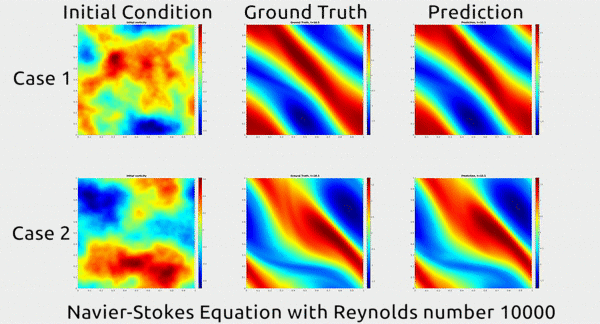
The GIF below shows an impressive demonstration. The first column depicts two snapshots of a fluid’s motion; the second depicts how the fluid moved in real life, while the third depicts how the neural network expected the fluid will move. It resembles the second in appearance.
When the function fits
The first thing to remember is that neural networks are feature approximators at their heart. (Wait, what?) They’re calculating the function, or set of math operations, that will transpose one number into the other when they train on a data set of paired inputs and outputs. Consider making a cat detector. The neural network is trained by give it a large number of images of cats and non-cat images (the inputs) and assigning a 1 or 0 to each group (the outputs). The neural network then seeks out the best function for converting each image of a cat to a 1 and every other image to a 0. That’s how it can access a new image and tell you if it’s a cat or not, using the function it found to calculate its answer and if its has a good training, it will get it right almost all of the time.This function approximation method happens to be exactly what is needed to solve a PDE. A function that best represents, for example, the motion of air particles in physical space and time.
How AI Solve Differential Equation Problem
In most cases, neural networks are trained to approximate functions between inputs and outputs specified in Euclidean space, which is represented by a graph with x, y, and z axes. This time, however, the researchers chose to describe the inputs and outputs in Fourier space, a special form of graph used to map wave frequencies. According to Anima Anandkumar, a Caltech professor who supervised the research alongside her colleagues Andrew Stuart and Kaushik Bhattacharya, the insight they drew from work in other fields is that something like air motion can actually be defined as a combination of wave frequenciesAt a macro level, the wind’s general direction is like a low frequency with very long, languid waves, while the micro level’s little eddies are like high frequencies with very rapid waves.
The reason why this matters is because it is much easier to approximate a Fourier function in Fourier space than it is to wrangle with PDEs in Euclidean space, the neural network’s job is greatly simplified. In addition to a significant speed advantage over traditional methods, their methodology achieves a 30% lower error rate when solving Navier-Stokes problems than previous deep-learning methods.
The researchers’ experiments revealed that previous deep-learning methods had to be trained separately for each form of fluid, while this one only needs to be trained once to handle all of them. It should be able to handle any earth composition when solving PDEs related to seismic activity, and every material type when solving PDEs related to thermal conductivity, though they haven’t tried it with other examples yet.
Super-simulation
This study was not carried out by the professors and their PhD students for the sake of academic curiosity. They want to apply AI to a wider range of fields. Anandkumar first agreed to take on the PDE challenge with her colleagues and students after speaking with a variety of collaborators in climate science, seismology, and materials science. They are now collaborating with other Caltech and Lawrence Berkeley National Laboratory researchers are now working to bring their approach into practice. It will now be helpful to see how far research has advanced in the field and how they can further apply this new type of deep learning approach to benefit society.
Climate change is one of the research topics that excite Anandkumar. The Navier-Stokes equation is used to model weather conditions as well as air turbulence. “Having good, fine-grained weather predictions on a global scale is such a challenging problem,” she says, adding that “we can’t do it at a global scale today even on the most powerfull supercomputer, So if we can use these methods to speed up the entire pipeline, that would be tremendously impactful.”
Reference















