Introduction
The strangest mathematical result in the paradox of infinite cloning is how we can turn a sphere into its own twin by repositioning its parts. Consider a situation where you and your friend are walking through the woods. You are hungry and decide to share an apple, but the part of the apple given to you seems thin. Then you think upon the strangest idea of mathematical infinity theorem that can, in principle at least, turn your apple into its identical copy. This principle is known as the Banach-Tarski paradox proposed by the mathematicians Alfred Tarski and Stefan Banach in the year 1924. The principle states that it is possible to break the given solid three-dimensional sphere into parts through which two identical copies could be obtained by recombination.
Infinite Cloning Paradox
Infinity may pretend to us like a number but in reality, it doesn’t act like one. On the other hand, the real numbers may include an infinite number of scales of decimal places when presented on the number line. In simple words, they could be considered as an uncountable infinity. We can’t even count the overall intervals in between the numbers 0 and 1. The distinction between the countable and uncountable infinities defines that the real numbers are infinitely larger than the natural numbers. This distinction among the numbers could be defined as the “cardinalities.” We can say that cardinality in reality is a very big term as compared to the simple Jiu-Jitsu. A famous mathematician Georg Cantor in the year 1891 suggested that the cardinality of infinite points of a volume is equivalent to the infinite points on a number line. Therefore, we can say that a sphere could be easily twisted in half by dividing the myriad endless rows of dots it contains. The dissection process is responsible for the separation occurring in the material.

Experimental Steps
We are required to pick a starting point to begin the creation of countable infinite sets. We may choose one of the sphere’s points and it is sufficient. Then we will select two angle measures like irrational degrees such as pi. In no time, we could spin the sphere. These two angle measures must correspond to east-west rotation and north-south rotation. Now, we are required to spin the ball by proper degrees either in the West, East, South, or North direction. We will then reach a new point on the sphere and this point will be marked as the second point. After that, we are required to roll the ball again in either direction, but on a condition that we would not backtrack in the previous direction i.e. if we went south, then we must not go North in the next step. In this way, we will obtain the third point of the set. These steps are required to be continued an infinite number of times so that we could obtain infinitely many points on the set.
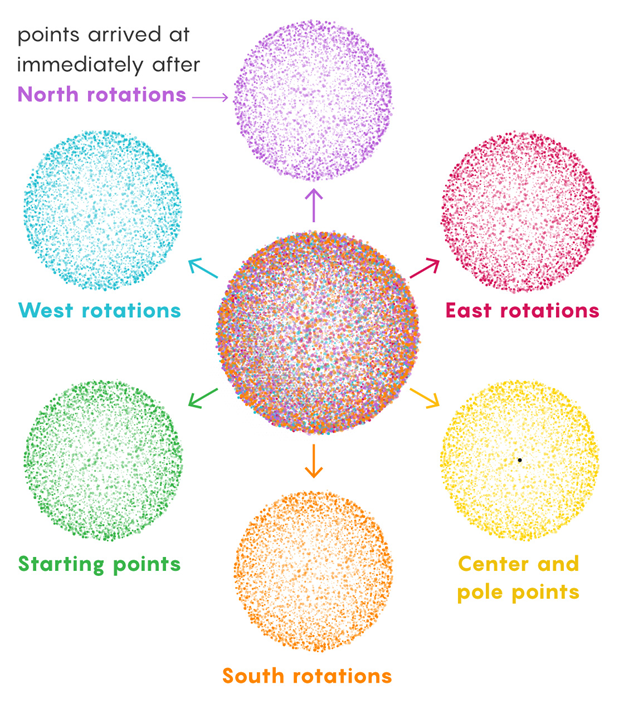
Properties of Infinite Cloning
The important function of these infinite numbers of points on the set is that the irrational number of angle rotations should be chosen assuring that the point recorded in the set must not repeat itself again and we must assign a natural number for every recorded point in the set. We must repeat these steps at each point on the ball. Each and every recorded point on the set is able to create its unique subsequent sets in the procedure. Hence, we can obtain innumerable infinite sets. Once we have successfully prepared the innumerable infinite sets, we are required to divide the points on the set into six groups namely North rotation points, South rotation points, East rotation points, West rotation points, starting points, and center and pole points, respectively.
Only one sphere would be obtained if we combine these six groups together. But, if we spin the points of a group, then we will obtain more points for the set. This will produce a larger set than the previous one.
Concept of Infinite Cloning
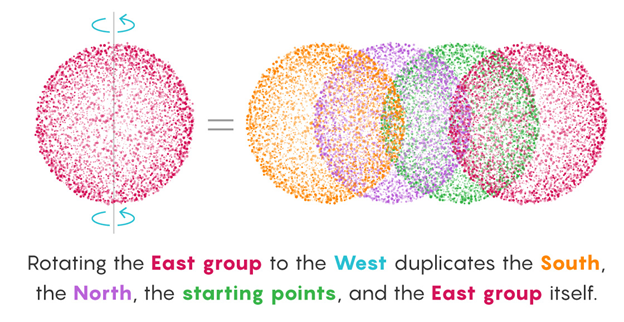
Let us consider an example where we choose the points from a group that was obtained via the last turn to the South direction. Now turn this group in the North direction. When we spin the South group points in the North direction, it will duplicate the East rotation points, West rotation points, starting points as well as South rotation points itself. In this way, we could easily obtain a new set that contains the previously recorded points as well as some new points on the set. At this point, we will be duplicating each and every group of points to form a new huge innumerable infinite set.

This could be better understood by an example of a hotel where there are infinite rooms for the guests. Let us consider a situation where only one room is vacant. We can provide that empty room to the infinite number of guests by shifting them all to the room above the vacant room and shifting them downwards one by one. Whenever the guest shifted in the vacant room leaves its place, the next guest takes its specific place and in this way, the infinite number of guests could be shifted to a single vacant room without creating more vacant space for them.

We could relate this example to our experiment by considering the missing poles set as a vacant room that dots the latitude line while filling the spaces in the duplicated sphere. These points could be easily shifted over the latitude line where the vacancies will be filled by an infinite number of points.
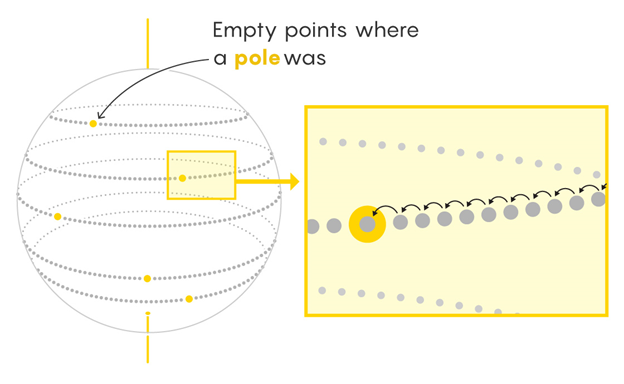
The free center is in another circle that can be easily filled by implementing the above steps. In this way, all six groups will be efficiently duplicated. Now we can put each group into their relevant sphere by combining the points in the set.
Conclusion
The result seems impossible. Every paradox has criticism. In this case, some consider it as an absurd conclusion. But this is a very big milestone in the field of mathematics that states that everything could be replicated or decomposed into its identical twin having the same cardinality as the original.
References:
Max G. Levy (26 August, 2021), “Banach-Tarski and the Paradox of Infinite Cloning”, retrieved from https://www.quantamagazine.org/how-a-mathematical-paradox-allows-infinite-cloning-20210826/
Terence Tao. An Introduction to Measure Theory. Graduate studies in mathematics. Los Angeles: American Mathematical Society, 2011, pp. 2–4. isbn: 9780821869192. url: https://books.google.se/books?id=HoGDAwAAQBAJ.
John R. Durbin. Modern Algebra: An Introduction. 6th Edition. Wiley, 2008. isbn: 9780470384435
Grzegorz Tomkowicz and Stan Wagon. The Banach–Tarski Paradox. 2nd Edition. Encyclopedia of Mathematics and its Applications. Cambridge: Cambridge University Press, 2016. doi: https://doi.org/10.1017/CBO9781107337145.
Tom Weston. “The Banach–Tarski Paradox”. 2003. url: https://people.math.umass. edu/~weston/oldpapers/banach.pdf. Søren Knudby. “The Banach–Tarski Paradox”. B.S. Thesis. [Accessed 2020 May 10]. University of Copenhagen, 2009. url: https://www.math.ku.dk/english/research/tfa/ncg/paststudents/bstheses/SK_bsthesis.pdf.
Donald L. Cohn. Measure Theory: Second Edition. Birkhäuser Advanced Texts Basler Lehrbücher. New York: Springer New York, 2013. isbn: 9781461469568. doi: https://doi.org/10.1007/978-1-4614-6956-8.
Omar A. Camarena. Lebesgue measure is invariant under isometries. [Cited 2020 May 9]. url: https://www.matem.unam.mx/~omar/notes/lebesgue.html.














