-By Rohan Purohit

Ever since we got to see the images of a real black hole we could not contain our excitement to find out what’s inside the monster. The answer, no one knows for sure. But one thing is for sure that when we get to know all about black holes, we will unlock the most mysterious secrets of the infinite cosmos. We will finally get to know how it all started and what was there before the ultimate big bang.

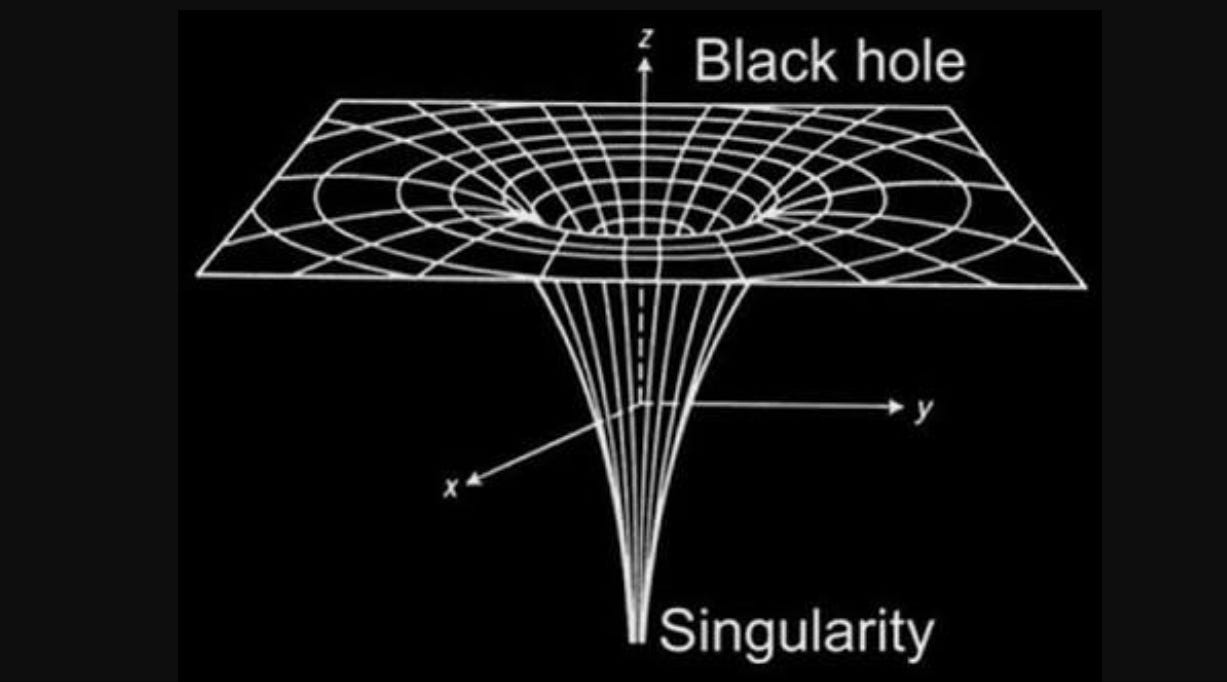
Most of the scientist has resolved a theoretical answer for this problem; they call it the gravitational singularity. In astrophysics, singularity refers to a location in space-time where the mass and gravitational field of a celestial body is predicted to be infinite by general relativity in a way that it does not depend on the coordinate system. The quantity that is used to measure the magnitudes of these things are scalar invariant curvatures of space-time, it also includes a measure of the density of matter. All such quantities become infinite, so normal laws of physics break down.

Gravitational singularity when considered with the context of general relativity, where magnitudes of mass and density become infinite at the centre of the black hole. Cosmologist and astrophysicist around the world anticipate that this must be the point where the big bang started or what was before the big bang. But as there is no proof about the existence of these singularities all the things said are just theoretical. Physicists at current state have insufficient knowledge and technology to deal with things that happen at such extreme densities.

The theory of general relativity predicts that such a thing must have existed before the creation of the universe, i.e. at the beginning of the big bang. Schwarzschild equation and theorems say that objects collapsing beyond a certain point (i.e. Schwarzschild radius for stars) would form a black hole, inside which a singularity will exist covered by the event horizon. As the singularity lies inside the event horizon and nothing can escape the event horizon not even light so, therefore, an outside observer cannot see it.

Today neither quantum mechanics nor general relativity can explain gravitational singularity and earliest movements of the big bang. But generally, quantum mechanics does not permit a particle to inhibit less space than its wavelength.

Interpretation and origin

Many theories in mathematics predict some kind or other singularities and in each case the proved one is different. Equations like theses brig theories that ball of a particular mass m tend to become infinite due to some reasons. There is always some missing pieces in the theory.

Other than that some theories like loop quantum gravity suggest that singularities might not exist. This is also true for the unified field theory of Einstein-Maxwell-Dirac equation. This idea can be stated through quantum gravity effect, as there is a minimum distance between two objects after which the gravitational force stops to increase.

TYPES OF SINGULARITIES

There are different types of singularities each with their different physical features. Some singularities were discovered first and some were found later on. Some singularities have event horizon wrapped in them and some singularities are found without any event horizon.

1. Conical singularity
2. Curvature singularity
3. Naked singularity

CONICAL SINGULARITY

A conical singularity occurs when there is a point where the limit of every diffeomorphism invariant quantity is finite, in which case space-time is not smooth at the point of the limit itself.  For this phenomenon, the space-time around it looks like a cone and the vary tip of the cone represents the singularity point. The metric can be finite every time a coordinate system is used.

An example of conical singularity is the cosmic string and a Schwarzschild black hole.

CURVATURE SINGULARITY

Answers for the hypothesis of supergravity or that of the overall relativity where the point experienced measurement explodes to endlessness. In any case, a large number of these focuses are normal, and the boundless qualities are just an aftereffect of utilizing a wrong facilitate framework now. To test whether there is a singularity at one point, one should check whether now diffeomorphism invariant amounts (for example scalars) become boundless. Such amounts are the equivalent in each arranges framework, so these vast qualities won’t “disappear” by a difference in directions.

A model is the Schwarzschild arrangement that portrays a non-pivoting, uncharged black hole. In organize frameworks helpful for working in areas far away from the black hole, a piece of the measurement gets limitless at the event skyline. In any case, space-time at the event skyline is customary. The consistency gets obvious when changing to another arrange framework, (for example, the Kruskal organizes), where the measurement is smooth. Then again, in the focal point of the black hole, where the measurement gets endless too, the arrangements propose a singularity exists.

While in a non-turning black hole the singularity happens at a solitary point in the model directions, called a “point singularity”, in a pivoting black hole, otherwise called a Kerr black hole, the singularity happens on a ring (a roundabout line), known as a “ring singularity”. Such a singularity may likewise hypothetically turn into a wormhole.

All the more, by and large, a space-time is viewed as of particular on the off chance that it is geodetically fragmented, implying that there are unreservedly falling particles whose movement can’t be resolved past a limited time, being after the purpose of arriving at the singularity. For instance, any eyewitness inside the event skyline of a non-pivoting black hole would fall into its middle inside a limited timeframe. The old-style rendition of the Big Bang cosmological model of the universe contains a causal singularity toward the beginning of time (t=0), where unsurpassed like geodesics have no expansions into the past.

NAKED SINGULARITY

Until the early 1990s, it was highly believed that naked singularities do not exist in reality. But general relativity explains that it can exist theoretically and is referred to as cosmic censorship hypothesis. However, in 1991, physicists Stuart Shapiro and Saul Teukolsky performed computer simulations of a rotating plane of dust that indicated that general relativity might allow for “naked” singularities. They still didn’t know how its visuals will be in its original model. However, it is hypothesized that light entering a singularity would similarly have its geodesics terminated. For which it is strongly believed that they might not have any event horizon and look exactly like normal black holes.

ENTROPY

The concept of black holes having certain entropy was new until Stephen hawkings came up with his thing called hawking’s radiation. This theory solved all the problems related to thermodynamics. This concept demonstrates that black holes radiate energy, which conserves entropy and solves the incompatibility problems with the second law of thermodynamics. The loss of energy also implies that black holes do not last forever, but rather evaporate or decay slowly. Blackhole temperature is inversely related to mass. All known black hole candidates are so large that their temperature is far below that of the cosmic background radiation, which means they will gain energy on the net by absorbing this radiation. They cannot begin to lose energy on the net until the background temperature falls below their temperature. This will occur at a cosmological redshift of more than one million, rather than the thousand or so since the background radiation formed.

REFERENCES

Hawking, S. W.; Penrose, R. (1970), “The Singularities of Gravitational Collapse and Cosmology”, Proc. R. Soc. A, 314 (1519): 529–548, Bibcode:1970RSPSA.314..529H, doi:10.1098/rspa.1970.0021 (Free access.)

Shapiro, Stuart L.; Teukolsky, Saul A. (1991). “Formation of naked singularities: The violation of cosmic censorship” (PDF). Physical Review Letters. 66 (8): 994–997. Bibcode:1991PhRvL..66..994S. doi:10.1103/PhysRevLett.66.994. PMID 10043968.

Robert M. Wald (1984). General Relativity. University of Chicago Press. ISBN 0-226-87033-2.

7167-0344-0. §31.2 The nonsingularity of the gravitational radius, and following sections; §34 Global Techniques, Horizons, and Singularity Theorems

Roger Penrose(1996). “Chandrasekhar, Black Holes, and Singularities”. ias.ac.in.

Roger Penrose (1999). “The Question of Cosmic Censorship”. ias.ac.in.

Τ. P. Singh. “Gravitational Collapse, Black Holes and Naked Singularities”.